Autonomous VIO for Quadrotor

This VIO (Visual Inertial Odometry) project involves trajectory planning, accurate tracking and state estimation through stereo vision to realize GPS-denied quadrotor autonomy. Once a quadcopter can accurately estimate its own state and use it for planning and control, the last step towards autonomy is to implement a mapping solution so the quadcopter can sense where the obstacles are using its on-board sensors. [code]

Approach

Trajectory Planning:

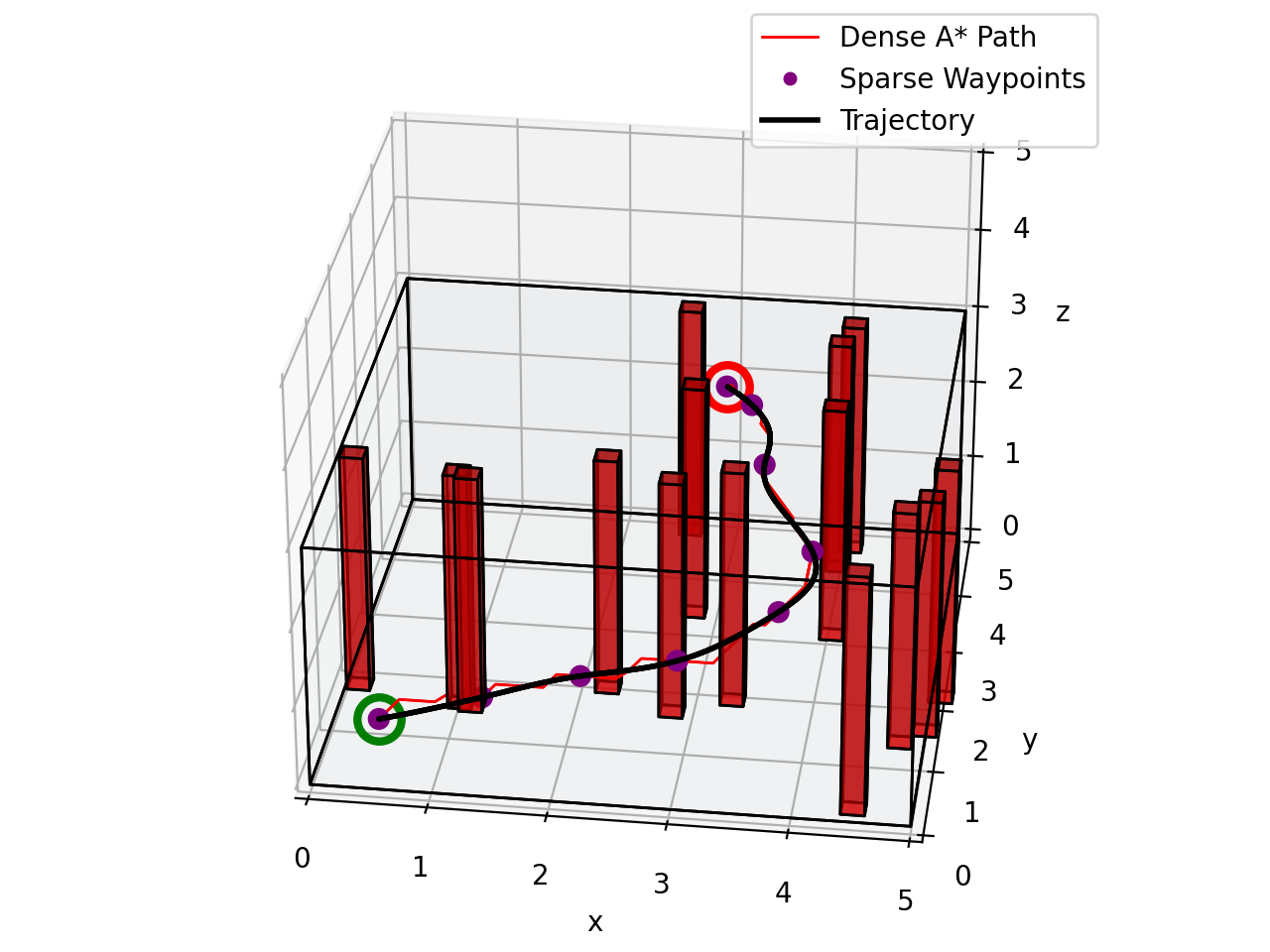
In the simulation, the map is assumed known and the start and the goal position is given ahead. In practice, when the whole map is unkown to the robot, the robot is expected to sense its surroundings by using its on-board sensors and plan the trajectories in real-time. In the planning phase, we make the following process:

• Discretizing the map into voxel grids
• A* algorithm to find the shortest path to the goal position
• Waypoints prune to elemenate shape turns and alleviate quadrotor overshoot
• Using Minimum Snap to interpolate between post-processed waypoints and generate the final smooth trajectory

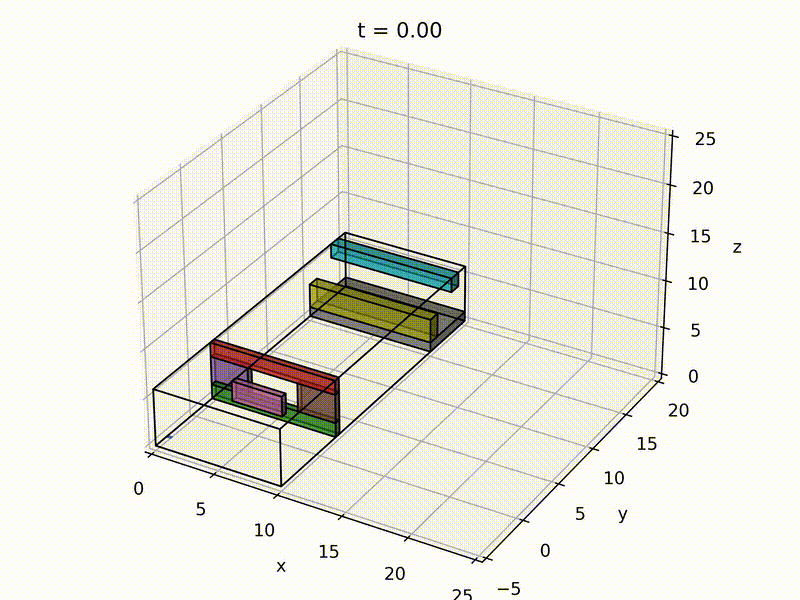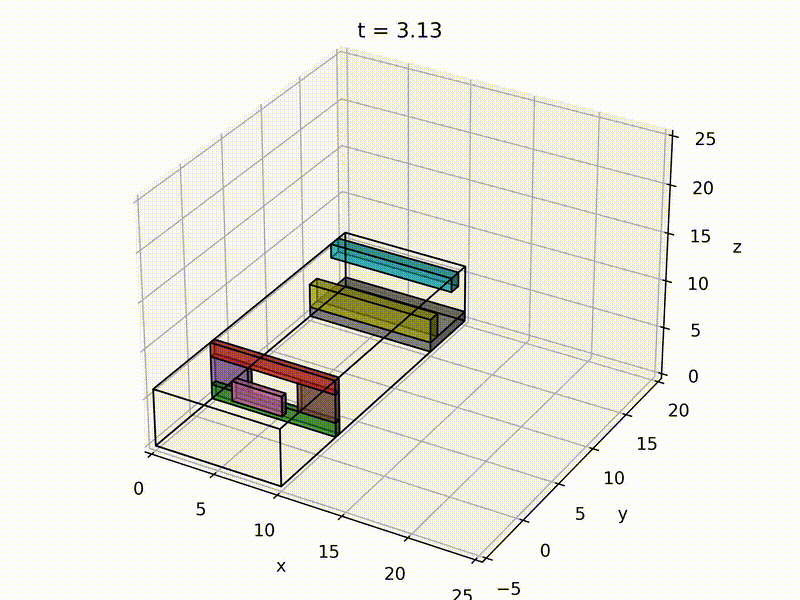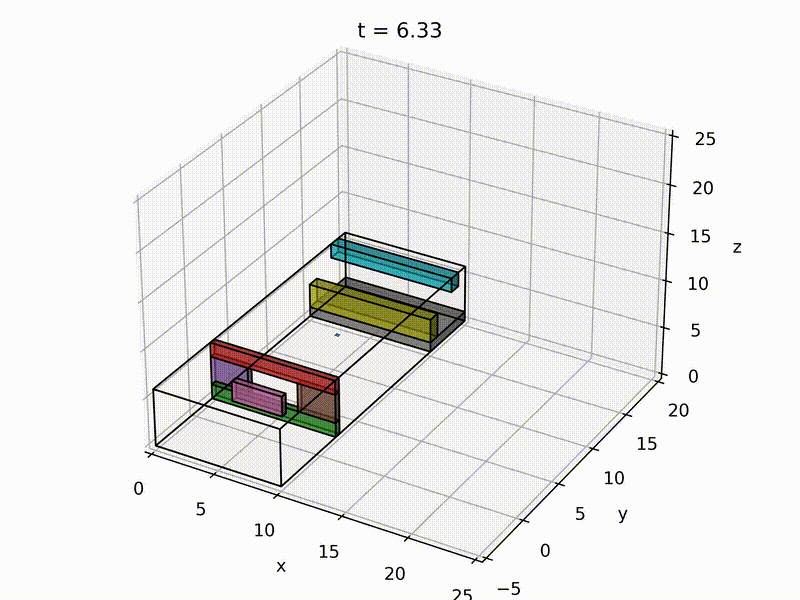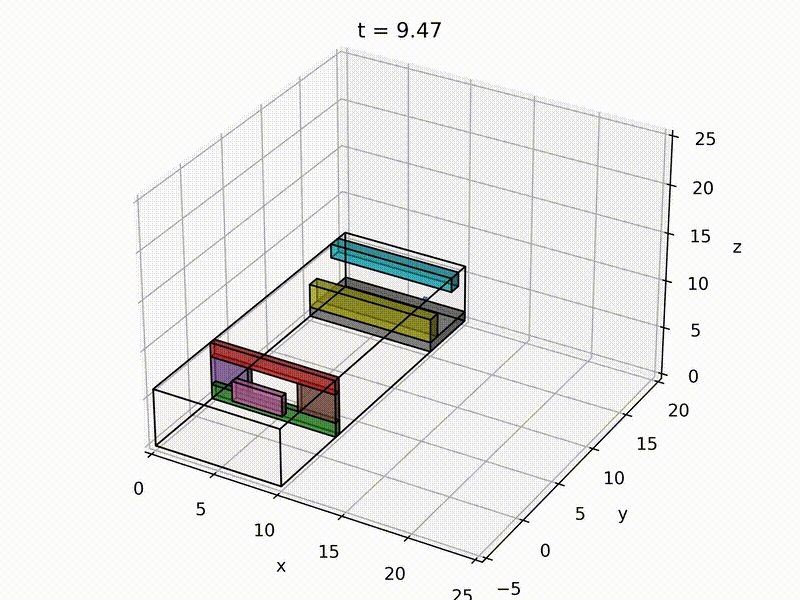
The following is an example:

Trajectory Tracking:

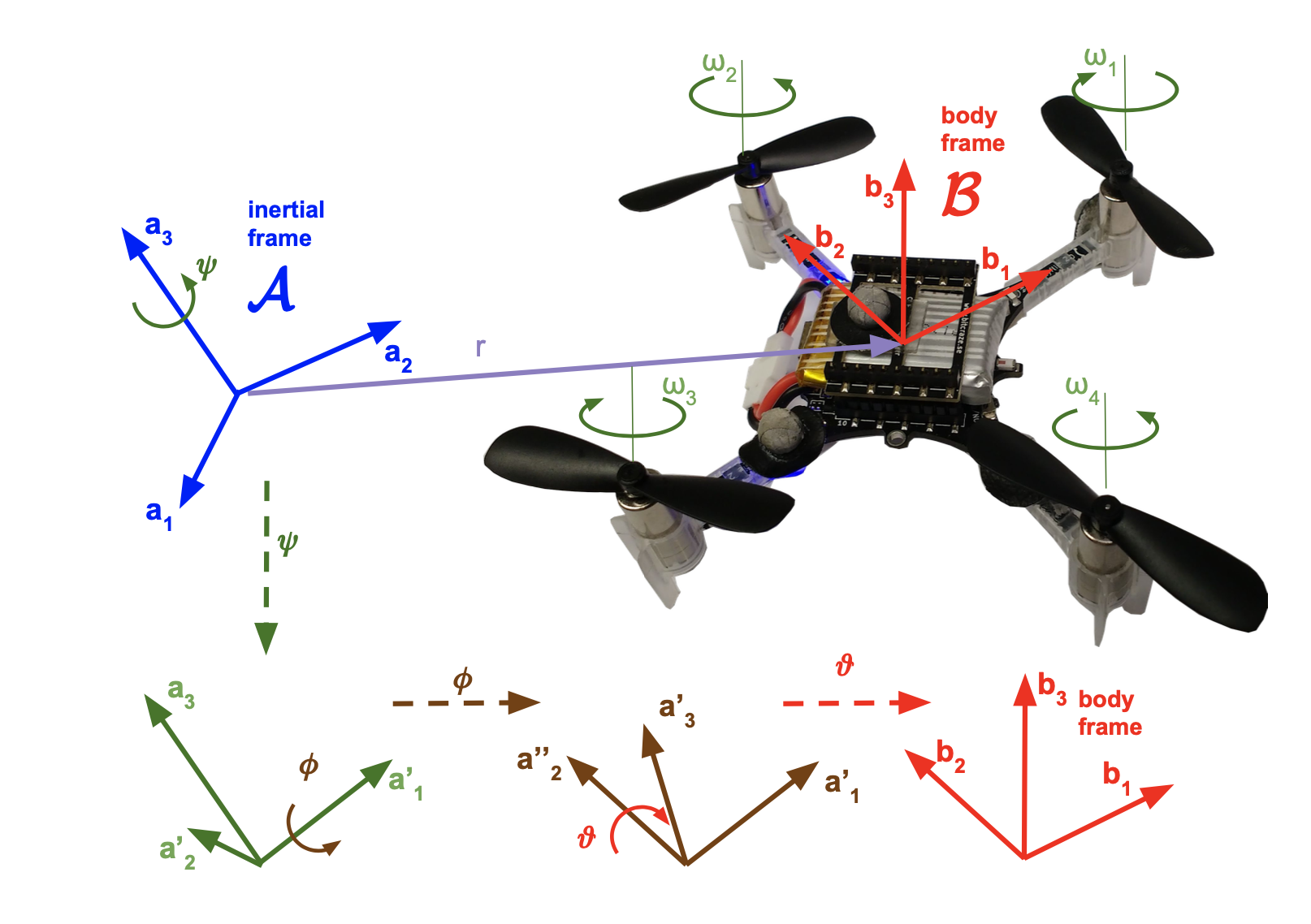
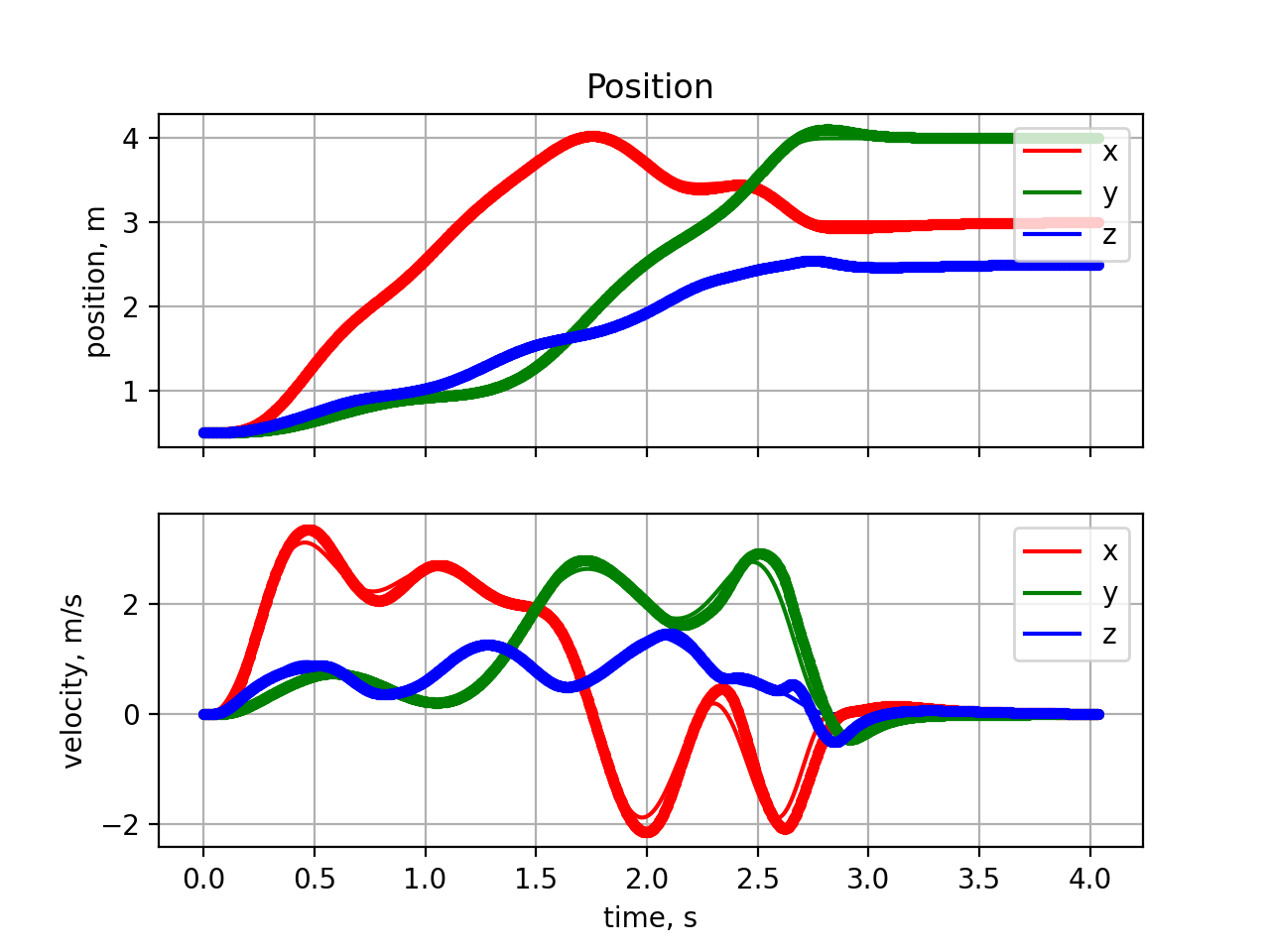
For quadrotor tracking, a Nonlinear Geometric Controller is designed in reference to Lee et al..

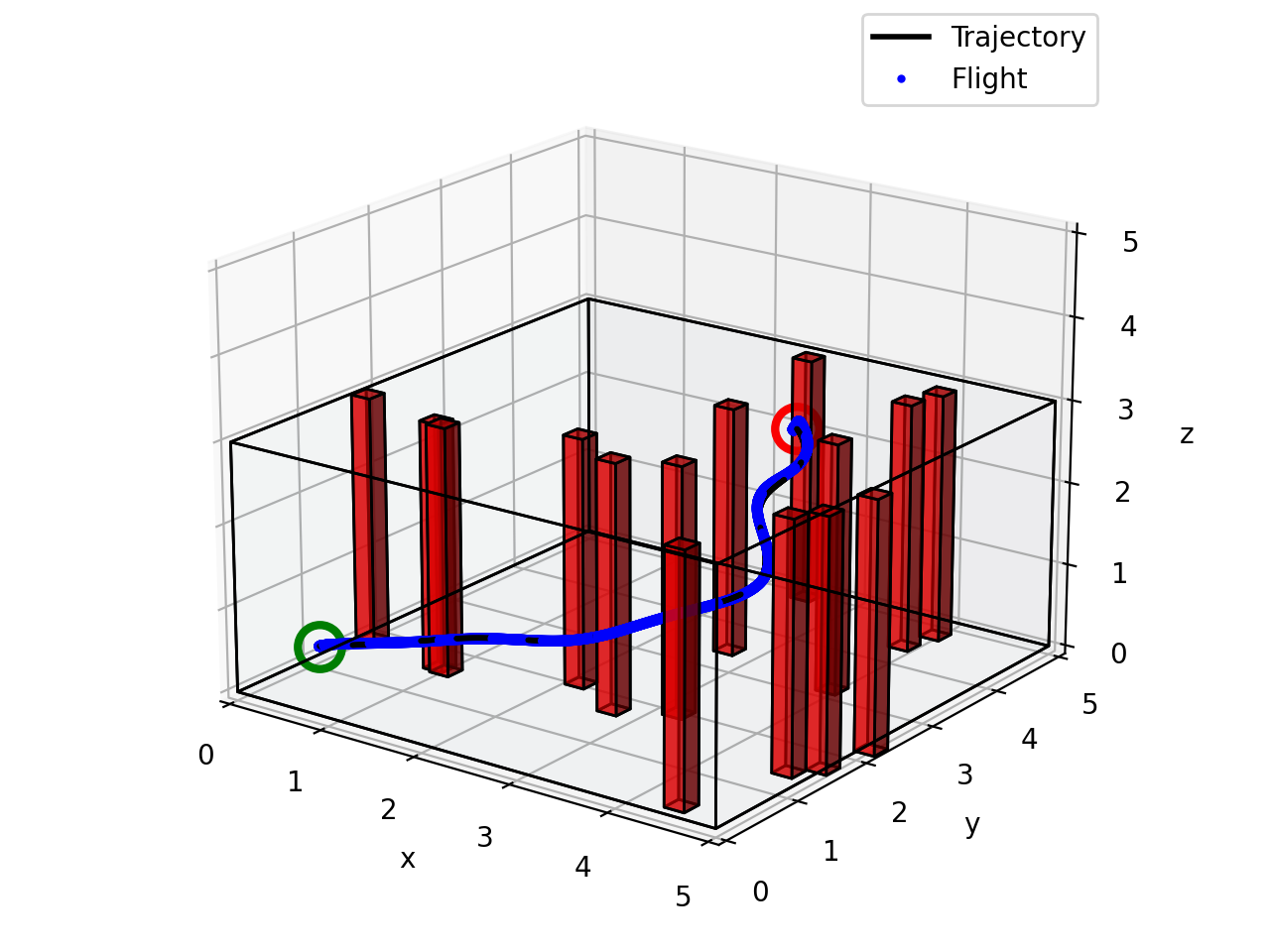
The performance of tracking control:

State Estimation:

In this setup, the on-board sensors are IMU and a stereo rig. A complementary filter is applied to estimate the attitude of a flying quadrotor based on data from a 6 axis IMU which provides acceleration and angular rate measurements. Given stereo vision, depth can be well extracted. Feature matching and RANSAC are then applied to estimate the pose of the quadrotor. Besides, an Error State Kalman Filter (ESKF) is specially designed for pose estimation. We proceed by incorporating every IMU update as a nonlinear state update to update our nominal model of the pose of the system \(x_n\). Since IMU updates are more frequently than vision updates, we use visual measurements to correct the state.